• DPOS机制
    • 前言
    • 源码
    • 类图
    • 数据库表
    • 解读
      • 拜占庭将军问题
      • 亿书DPOS机制概述
      • 1.注册受托人
      • 2.投票
      • 3.块（时段）周期（Slots）
      • 4.受托人（循环）周期（Round）
      • 5.奖励周期（Milestones）
  • 总结
  • 参考

    DPOS机制

    前言

    共识机制是分布式应用软件特有的算法机制。在中心化的软件里，再复杂的问题都可以避开使用复杂的算法逻辑（当然，如果能用算法统领，代码会更加简洁、高效），在开发设计上可以省却一定的麻烦。但在分布式软件开发中，节点间的互操作，节点行为的统一管理，没有算法理论作为支撑，根本无法实现。所以，要想开发基于分布式网络的加密货币，共识机制无法回避。

    在第一个部分，专门用一篇文章《共识机制，可编程的“利益”转移规则》来介绍共识机制的作用，也对比了当前加密货币领域常用的三种共识算法原理和优越点，但是并没有对共识算法进行深入讨论。这一篇我们就从解释“拜占庭将军问题”开始，来探讨加密货币的算法问题，并通过代码学习和研究亿书共识机制的具体实现。

    源码

    主要源码地址：

    delegates.js https://github.com/Ebookcoin/ebookcoin/blob/v0.1.3/modules/delegates.js

    round.js https://github.com/Ebookcoin/ebookcoin/blob/v0.1.3/modules/round.js

    accounts.js https://github.com/Ebookcoin/ebookcoin/blob/v0.1.3/modules/accounts.js

    slots.js: https://github.com/Ebookcoin/ebookcoin/blob/v0.1.3/helpers/slots.js

    类图

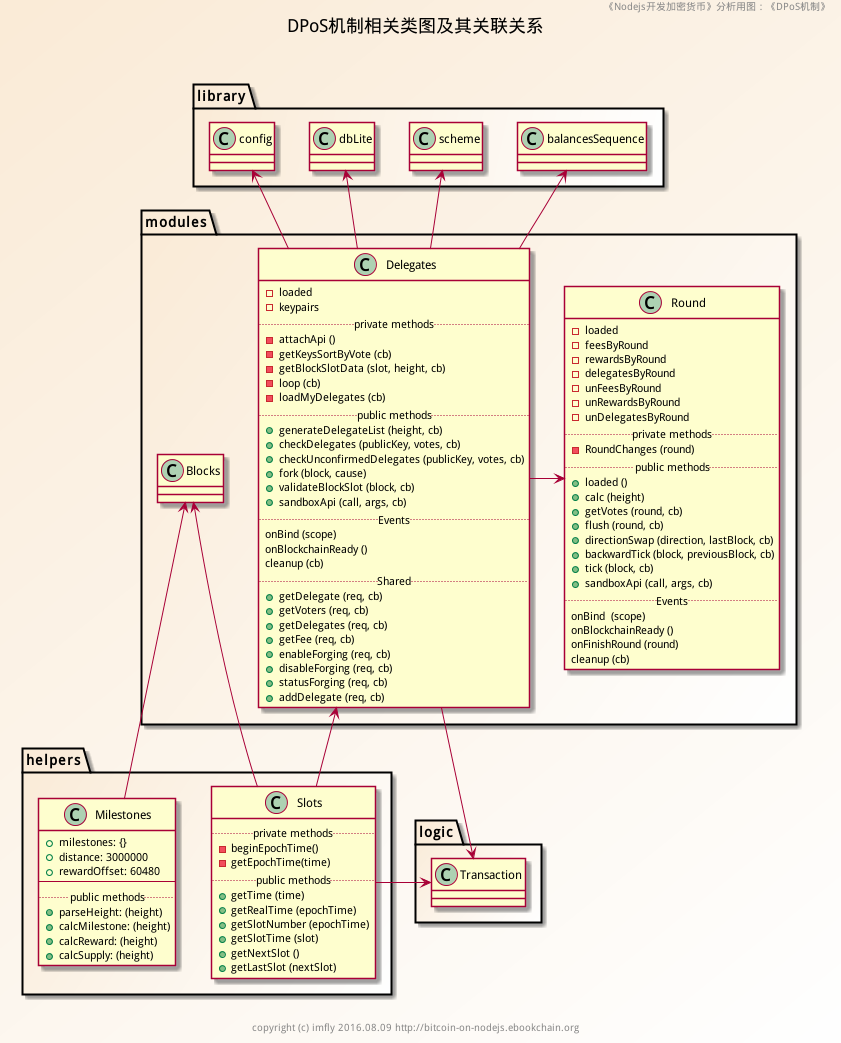
    dpos-class.png

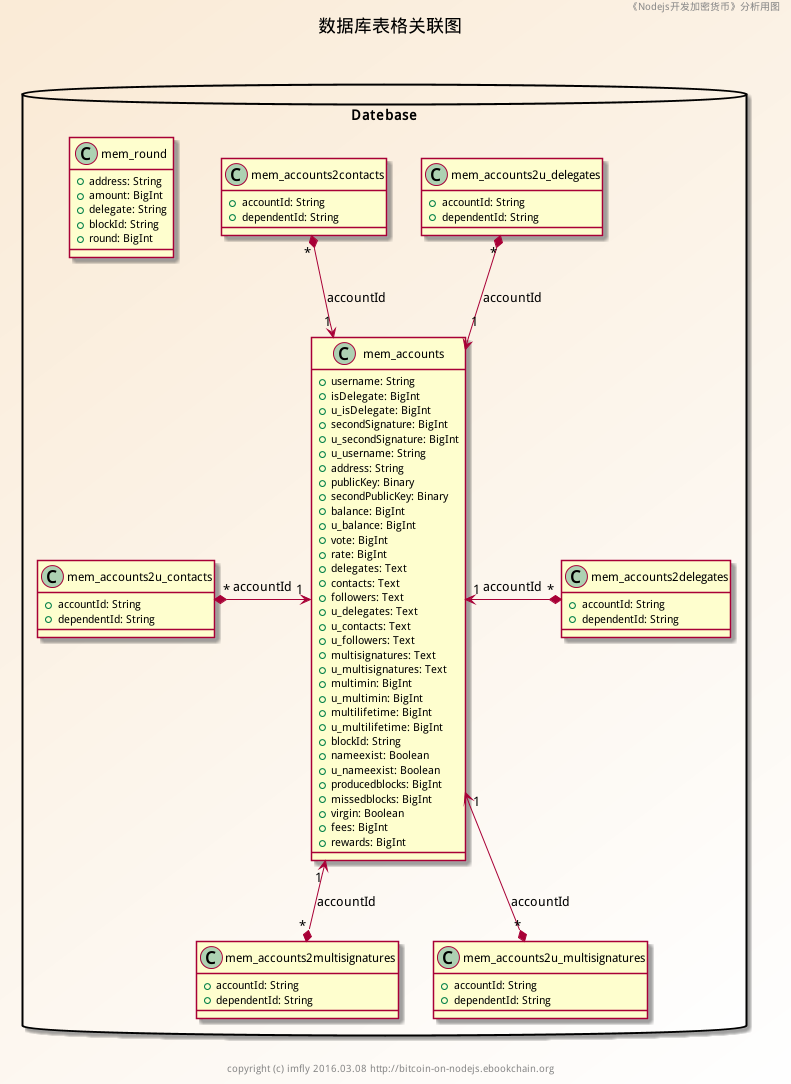
    数据库表

    整个数据库表应该都在该机制的管理之下，不过与用户相关的是与之直接关联的，特别是 mem_round 表。

    dpos-database.png

    解读

    在币圈如果不知道“拜占庭将军问题”，那说明您还没有发现问题的本质。但是要想理解这个问题，如果没有点高等数学和计算机编程基础，也不是非常简单的事情。我们这里就从八卦讲起，扒扒这个概念的由来，然后对照比特币的解决办法，引出亿书机制的实现。

    拜占庭将军问题

    （1）比特币是怎么来的？

    这里咱也八卦一下，猜猜比特币如何诞生的。在学习一门新技术的时候，我们通常会好奇，发明这项新技术的人，他是怎么想到要进行这项发明的呢？同样，对于比特币，我也曾经好奇，中本聪怎么想到要发明比特币的呢？这大量高科技的应用，可不是个小工程，一定要有明确的目的才行。这种好奇，始终督促我不断研究下去。

    算法是解决问题的理论基础，拜占庭将军问题就是针对分布式共识算法提出来的，而这个问题也是比特币等加密货币的核心问题。根据比特币白皮书（更像一篇科技论文吧）内容描述，大量篇幅提到诚实节点、攻击者等问题，类似于古代战场攻防对战，很多人猜测中本聪或许就是一位专门研究这个方向的大学老师或研究人员，他解决了这个问题，推出了相关论文，并根据研究成果写出了产品原型——比特币。所以，才会说比特币仅仅是一项实验。

    显然，这种猜测，纯属马后炮，由结果找原因，毫无历史根据。网上搜索了一下，各种猜测还真不少。姑且避开八卦内容，其中比较有价值的，是一篇比特金（Bit Gold）白皮书，因为它与比特币有惊人的相似之处，因此其开发者尼克·萨博（Nick Szabo）被认为最有可能是中本聪本人。比特金比比特币要早，它的目标就是实现一种不需要（只需极小的）信用中介的电子支付系统，与比特币的目标基本一致。

    可见，通过使用点对点网络、加密解密等技术实现加密货币的研究由来已久，可以肯定的是，比特币的初衷绝非单纯为了解决拜占庭将军问题那么简单。相反，为了实现没有中介的电子支付系统而设计倒是更加合情合理，只不过附带完美的解决了拜占庭将军问题而已。事实上，比特币算是解决拜占庭将军问题的一个完美实现。

    （2）什么是拜占庭将军问题？

    但不管怎么说，拜占庭将军问题是比特币无法逾越的问题。该问题最早是由Leslie Lamport解决，为了提高宣传效果，老先生在研究论文里编造了这么一个故事，事实证明非常成功，这个故事被广泛传播。故事内容是这样的：拜占庭是东罗马帝国的首都，为了防御外敌入侵，周边驻扎了军队，而且每个军队都分隔很远，相互独立，将军与将军之间只能靠信差传递消息。在战争的时候，拜占庭军队内所有将军必需达成一致的共识（进攻或撤退），才有胜算把握。但是，在军队内部有可能存在叛徒，左右将军们的决定。这时候，在已知有成员叛变的情况下，其余忠诚的将军如何达成一致的协议，拜占庭问题就此形成。Lamport 证明了在理想状态下，背叛者为m或者更少时，将军总数只要大于3m，忠诚的将军就可以达成一致。

    从技术上理解，拜占庭将军问题是分布式系统容错性问题。加密货币建立在P2P网络之上，是典型的分布式系统，类比一下，将军就是P2P网络中的节点，信使就是节点之间的通信，进攻还是撤退的决定就是需要达成的共识。如果某台独立的节点计算机拓机、掉线或攻击网络搞破坏，整个系统就要停止运行，那这样的系统将非常脆弱，所以容许部分节点出错或搞破坏而不影响整个系统运行是必要的，这就需要算法理论上的支撑，保证分布式系统在一定量的错误节点存在的情况下，仍然保持一致性和可用性。

    我非常赞同把拜占庭将军问题与两军问题分开，两个问题的本质不同，后者重在研究信差的通信问题，类似于TCP协议的握手操作，原则上是没有解的。而拜占庭将军问题是假定信差没有问题，只是将军出现了叛变等问题，所以二者本质有区别。不过，在实际的加密货币系统里，信差的问题，比如通信中断、被劫持等，都可以归为将军（节点）出了问题，理解到这一点就可以了，因此可以说比特币是完美解决了这两个问题。关于两者的区别，请看这篇文章《拜占庭将军问题深入探讨》（见附件），作者下了不少功夫，值得一读。

    （3）比特币是如何解决拜占庭将军问题的？

    Lamport 给出了理想状态下的答案，但现实是复杂的，比特币是如何解决的呢？事实上，比特币通过“工作量证明”（PoW）机制，简单的规范了节点（将军）的动作，从而轻松解决这个问题：

    首先，维持周期循环，保证节点步调一致。这个世界上，最容易达成的就是时间上的共识，至少“几点见面”、“什么时候谈判”这样的问题很好解决吧，不然其他的都不用谈了。比特币有一个算法难度，会根据全网算力自动调整，以保证网络一直需要花费10分钟来找到一个有效的哈希值，并产生一个新区块。在这10分钟以内，网络上的参与者发送交易信息并完成交易，最后才会广播区块信息。拜占庭将军问题复杂在将军步调不一致，比特币杜绝了节点（将军们）无限制、无规律的发送命令的状态。

    其次，通过算力竞赛，确保网络单点广播。将军们如果有个“带头大哥”，事情就好办了。这里的“带头大哥”可以简单的竞争得来，举个极端的例子，说好的8点钟谈判，那么先到的就是“带头大哥”，可以拟定草稿，等其他人到了签字画押就行了。 “工作量证明”就是一种竞赛机制，算力好的节点，会最先完成一个新区块，在那一刻成为“带头大哥”。它把区块信息立即广播到网络，其他节点确认验证就是了。比特币通过时间戳和电子签名，实现了这样的功能，确保在某一个时间点只有一个（或几个，属于分叉行为）节点传输区块信息，改变了将军们互相传送的混乱。

    最后，通过区块链，使用一个共同账本。对于单个区块，上述两条已经可以达成共识了。但现在的问题是，有一个叛徒（不诚实节点）修改了前面区块的信息，计划把钱全部划归自己所有，当它广播新区块的时候，其他节点如何通过验证？如果大家手里没有一份相同的账本，肯定无法验证，问题就会陷入僵局。基于P2P网络的BT技术是成熟的，同步一个总帐是很简单的事情。网络中的节点，在每个循环周期内都是同步的，这让每个节点（将军）做决策的时候就有了共同的基础。如果每个节点都独立维护自己的账本，问题的复杂性将无法想象，这是更广泛基础上的共识。

    上述三点内容是比特币“工作量证明”（PoW）机制解决拜占庭将军问题的答案，也为其他竞争币提供了重要参考。事实上，无论你采取什么样的方式，只要保证时间统一、步调一致、单点广播、一个链条就能解决加密货币这种分布式系统的拜占庭将军问题。如果还不能深刻理解这其中的奥妙，下面，就让我们通过阅读亿书源码，来研究DPOS（授权股权证明）机制的具体实现，去直观感受一下吧。

    亿书DPOS机制概述

    [亿书白皮书][] 描述了DPOS（授权股权证明）机制基本原理和改进方法，这里不再重复。亿书由受托人来创建区块，受托人来自于普通用户节点，需要首先进行注册，然后通过宣传推广，寻求社区信任并投票，获得足够排行到前101名的时候，才可以被系统接纳为真正可以处理区块的节点，并获得铸币奖励。比特币是通过计算机算力来投票，算力高的自然得票较多，容易获胜。DPOS机制是通过资产占比（股权）来投票，更多的加入了社区人的力量，人们为了自身利益的最大化会投票选择相对可靠的节点，相比更加安全和去中心化。整个机制需要完成如下过程：

    （1）注册受托人，并接受投票

    • 用户注册为受托人;
    • 接受投票（得票数排行前101位）;

    （2）维持循环，调整受托人

    • 块周期：也称为时段周期（Slot），每个块需要10秒，为一个时段（Slot）；
    • 受托人周期：或叫循环周期（Round），每101个区块为一个循环周期（Round）。这些块均由101个代表随机生成，每个代表生成1个块。一个完整循环周期大概需要1010秒(101x10)，约16分钟；每个周期结束，前101名的代表都要重新调整一次；
    • 奖励周期：根据区块链高度，设置里程碑时间（Milestone），在某个时间点调整区块奖励。

    上述循环，块周期最小（10秒钟），受托人周期其次（16分钟），奖励周期最大（347天）。

    （3）循环产生新区块，广播

    产生新区块和处理分叉等内容，上一章《区块链》已经讲过，这里不再赘述。

    下面，我们通过源码逐个查看其实现方法。

    1.注册受托人

    注册受托人必须使用客户端软件（币圈俗称钱包），因此这项功能需要与节点进行交互，也就是说客户端要调用节点Api。管理受托人的模块是 modules/delegates.js ，根据前面篇章的经验，我们很容易找到该模块提供的Api：

    1. "put /": "addDelegate"

    最终的Api信息如下：

    1. put /api/delegates

    对应的方法是，modules/delegates.js模块的addDelegate()方法。该方法与注册用户别名地址等功能性交易没有区别，注册受托人也是一种交易，类型为“DELEGATE”（受托人），详细过程请自行查看modules/delegates.js文件1017行的源码，逻辑分析请参考《交易》等相关章节内容。

    2.投票

    我们在《交易》一章提到过，有一种交易叫VOTE，是投票交易类型。所有这类功能性交易的逻辑都很类似，就不再详细描述。这里要提示的是，该功能是普通用户具备的功能，任何普通用户都有投票权利，所以放在帐号管理模块，即“modules/accounts.js”文件里，是符合逻辑的，请参阅该文件729行的“addDelegates()”方法。当然，从代码实现上来说，放在modules/delegates.js文件里，或其他地方也都可以实现相同功能，只是逻辑上稍显混乱而已。

    3.块（时段）周期（Slots）

    （1）时间处理

    比特币的块周期是10分钟，由工作量证明机制来智能控制，亿书的为10秒钟，仅仅是时间上的设置而已，源码在helpers/slots.js里。这个文件非常简单，时间处理统一使用UTC标准时间（请参考开发实践部分《关于时间戳及相关问题》一章），创世时间beginEpochTime()和getEpochTime(time)两个私有方法定义了首尾两个时间点，其他的方法都是基于这两个方法计算出来的时间段，所以不会出现时间上不统一的错误。

    （2）编码风险

    但是，唯一可能出现错误的地方，就是getEpochTime(time)方法，看下面代码的16行，new Date() 方法获得的是操作系统的时间，这个是可以人为改变的，一般情况下不会有什么影响，但个别情况也可能引起分叉行为（上一篇文章《区块链》分析过分叉的原因，其中一个就发生在这里）

    1. // helpers/slots.js
    2. function getEpochTime(time) {
    3.     if (time === undefined) {
    4.       // 16行
    5.       time = (new Date()).getTime();
    6.     }
    7.     var d = beginEpochTime();
    8.     var t = d.getTime();
    9.     return Math.floor((time - t) / 1000);
    10. }

    （3）周期实现

    从现在时间点到创世时间，有一个时间段，大小假设为 t，那么 t/10 取整，就是当前时段数（getSlotNumber()）），这里的10是由 constants.slots.interval 设定的，见文件 helpers/constants.js 25行。

    具体到一个受托人，它处理的区块时段值相差应该是受托人总数，这里是101, 这个值由 constants.delegates 设定，见文件 helpers/constants.js 22行。因此，getLastSlot()方法（helpers/slots.js文件 54行）返回的是受托人最新时段值。

    （4）如何使用？

    块周期，是其他周期的基础，但是这里的代码并不包含任何区块、交易等关键信息。这里隐含的关联关系，就是区块、交易等信息的时间戳。只要知道任何一个时间戳，其他信息就可以使用这里的方法简单计算出来。典型的使用就是 modules/delegates.js 文件里的方法 privated.getBlockSlotData() 方法（470行），代码已在《区块链》一章贴出过，该方法为新区块提供了密钥对和时间戳。

    另外，在《区块链》一章，我们也指出，程序设定每秒钟（744行1000毫秒）调用一次“privated.loop()”方法用来产生新区块，但是因为loop()方法并非每次都能成功运行，所以实际运行起来是在10秒内找到需要的受托人并产生一个区块。

    （5）参数可调整吗？

    很多小伙伴问，为什么一定是10秒，其他的值可以吗？为什么要101个受托人，201个可以吗？回答都是可以。我认为这个块周期如果提高到20或30或许更好（需要验证），可能更有利于SQLite数据库，也自然降低了通胀比率（后面分析）。对于计算机而言，数据库IO操作是耗时大户，10秒间隔可以提高处理交易的数量，但也会造成数据库IO无法正确完成，所以这个值是压力测试的经验值。

    至于受托人的数量，也是如此。使用极限思维的方法，让受托人数量减少到1，效率高了，但是单点系统很容易受到攻击，安全性受到威胁；增加到无限大，那么查找受托人的方法将一直运行下去，结果是系统性能降到了0。所以，这个数字也是一个经验值，可以根据实际情况做适当调整。特别是那些要做DApp市场的应用，更应该考虑适当变更。

    4.受托人（循环）周期（Round）

    为了安全，亿书规定受托人每轮都要变更，确保那些不稳定或者做坏事的节点被及时剔除出去。另外，尽管系统会随机找寻受托人产生新块，但是在一个轮次内，每个受托人都有机会产生一个新区块（并获得奖励）并广播，这一点与比特币每个节点都要通过工作量证明机制（PoW）竞争获得广播权相比，要简化很多。

    这样，亿书每个区块都会与特定的受托人关联起来，其高度(height)和产生器公钥(generatorPublicKey)必是严格对应的。块高度可以轻松找到当前块的受托人周期（modules/round.js 文件51行的calc()方法），generatorPublicKey代表的就是受托人。而单点广播的权限也自然确定，具体代码见 modules/round.js 文件。

    这里，需要重点关注的是该文件的 tick() 和 backwardTick() 方法。tick，英文意思是“滴答声或做标记”，如果大家开发过股票分析软件，在金融领域，tick还有数据快照的涵义，意思是某个时段的交易数据。我个人觉得，这里就是这个意思，是指在一个受托人周期内某个受托人的数据快照。相关数据存储在 mem_round 表里，程序退出时就会被清空。具体代码如下：

    1. // modules/round.js
    2. // 224行
    3. Round.prototype.tick = function (block, cb) {
    4.     ...
    5.   // 229行
    6.     modules.accounts.mergeAccountAndGet({
    7.         publicKey: block.generatorPublicKey,
    8.         producedblocks: 1,
    9.         blockId: block.id,
    10.         round: modules.round.calc(block.height)
    11.     }, function (err) {
    12.         ...
    13.         if (round !== nextRound || block.height == 1) {
    14.             if (privated.delegatesByRound[round].length == constants.delegates || block.height == 1 || block.height == 101) {
    15.                 var outsiders = [];
    16.         // 255行
    17.                 async.series([
    18.           // 256行 找到那些没在当前轮次里的节点
    19.                     function (cb) {
    20.                         if (block.height != 1) {
    21.               // 258行 generateDelegateList()方法可以查询数据库里投票排行前101的节点，不过当前可能已经改变，这里把它们找出来
    22.                             modules.delegates.generateDelegateList(block.height, function (err, roundDelegates) {
    23.                                 ...
    24.                                 for (var i = 0; i < roundDelegates.length; i++) {
    25.                                     if (privated.delegatesByRound[round].indexOf(roundDelegates[i]) == -1) {
    26.                                         outsiders.push(modules.accounts.generateAddressByPublicKey(roundDelegates[i]));
    27.                                     }
    28.                                 }
    29.                                 ...
    30.                     },
    32.           // 把缺失的块暂时保存到 mem_accounts 表里
    33.                     function (cb) {
    34.                         if (!outsiders.length) {
    35.                             return cb();
    36.                         }
    37.                         var escaped = outsiders.map(function (item) {
    38.                             return "'" + item + "'";
    39.                         });
    40.                         library.dbLite.query('update mem_accounts set missedblocks = missedblocks + 1 where address in (' + escaped.join(',') + ')', function (err, data) {
    41.                             cb(err);
    42.                         });
    43.                     },
    45.           // 一开始就通过merge()方法向 mem_round 表添加了记录，这里 getVotes() 方法查询出来，并依次更新到 mem_accounts 表里。
    46.                     function (cb) {
    47.                         self.getVotes(round, function (err, votes) {
    48.                             ...
    49.                             async.eachSeries(votes, function (vote, cb) {
    50.                                 library.dbLite.query('update mem_accounts set vote = vote + $amount where address = $address', {
    51.                                     address: modules.accounts.generateAddressByPublicKey(vote.delegate),
    52.                                     amount: vote.amount
    53.                                 }, cb);
    54.                 ...
    55.                         });
    56.                     },
    58.           // 上述变化处理完毕，接着处理余额、费用和奖励变化
    59.                     function (cb) {
    60.                         var roundChanges = new RoundChanges(round);
    62.                         async.forEachOfSeries(privated.delegatesByRound[round], function (delegate, index, cb) {
    63.                             var changes = roundChanges.at(index);
    65.                             modules.accounts.mergeAccountAndGet({
    66.                                 publicKey: delegate,
    67.                                 balance: changes.balance,
    68.                                 u_balance: changes.balance,
    69.                                 blockId: block.id,
    70.                                 round: modules.round.calc(block.height),
    71.                                 fees: changes.fees,
    72.                                 rewards: changes.rewards
    73.                             }, function (err) {
    74.                                 ...
    75.                     },
    77.           // 最后，再一次更新 mem_accounts 的投票数据，没有问题就结束本轮循环（推送客户端改变），并清除 mem_round 记录的信息
    78.                     function (cb) {
    79.                         self.getVotes(round, function (err, votes) {
    80.                             ...
    81.                             async.eachSeries(votes, function (vote, cb) {
    82.                                 library.dbLite.query('update mem_accounts set vote = vote + $amount where address = $address', {
    83.                                     address: modules.accounts.generateAddressByPublicKey(vote.delegate),
    84.                                     amount: vote.amount
    85.                                 }, cb);
    86.                             }, function (err) {
    87.                                 library.bus.message('finishRound', round);
    88.                                 self.flush(round, function (err2) {
    89.                                     cb(err || err2);
    90.                                 });
    91.                             })
    92.                         });
    93.                     }
    94.                 ], function (err) {
    95.                     ...

    229行，modules.accounts.mergeAccountAndGet() 方法实际上是调用 logic/account.merge() 方法（见文件logic/account.js 请自行查阅），把这里的数据插入到 “mem-”开头的数据库表里，用于处理与账户相关的一些数据，该方法比较混乱，系统需要频繁处理，对性能有较大影响，亿书将在以后的版本里做进一步优化。

    255行，使用async.series方法，顺序执行了一些函数，具体情况请看代码中的注释，不再赘述。

    backwardTick() 方法是反方向处理，属于回退操作，请自行查阅分析。

    5.奖励周期（Milestones）

    该周期主要针对块奖励进行设置，与比特币的块奖励每4年减半类似，亿书的块奖励也会遵循一定规则。大致的情况是这样的，第一阶段（大概1年）奖励5EBC（亿书币）/块，第二年奖励4EBC（亿书币）/块，4年之后降到1EBC(亿书币)/块，以后永远保持1EBC/块，所以总量始终在少量增发。（亿书正式上线的产品可能会做适当调整，这里仅作测试参考）

    具体增发量很容易计算，第一阶段时间长度 = rewards.distance 10秒 / （24 60 60） = 347.2天，增发量 = rewards.distance 5 = 3000000 * 5 = 1500万。第二阶段1200万，第三阶段900万，第四阶段600万，以后每阶段300万。这种适当通胀的情况是DPoS机制的一个特点，也是为了给节点提供奖励，争取更多用户为网络做贡献。

    很多小伙伴担心这种通胀，会降低代币的价值，影响代币的价格。事实上，对于拥有大量侧链应用（下一篇介绍）的平台产品来说，一定要保证有足够代币供各侧链产品使用，不然会造成主链和侧链绑定紧密，互相掣肘，对整个生态系统都不是好事情。这种情况可以通过最近以太坊的运行情况体会出来，特别是侧链应用使用主链代币众筹时更不必说，此消彼长，价格波动剧烈。

    具体代码见文件 helpers/milestones.js，该文件编码很简单，都是一些算术运算，请自行浏览。这里简单给出流程图：

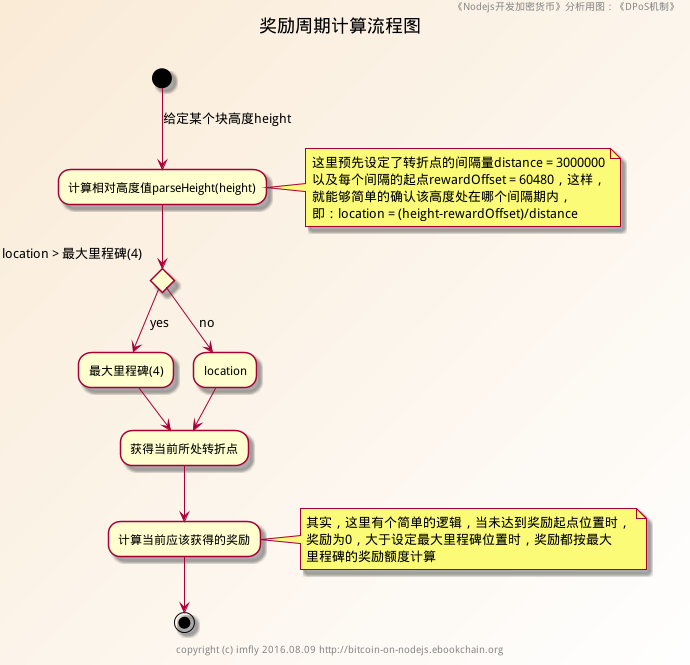
    milestones-activity.png

    唯一需要提醒的是，代码有一处非常隐晦的Bug，就是涉及到parseInt()方法的使用（请参考开发实践部分《Js对数据计算处理的各种问题》一章），特别是第26行。不过对系统的影响非常细微，仅仅在某个别区块高度的时候才会出现几次，比如：出现类似 parseInt(2/300000000) = 6 的情况。（亿书将在后面的版本中修改）

    总结

    本人介绍了拜占庭将军问题及比特币解决思路，也沿着这个思路阅读了亿书相关源码，内容涉及到多个源文件。其中，大量的细节因为篇幅所限没有详细提供，需要小伙伴们自己查阅。从源码设计上来说，这一部分的源码还需要更多的优化设计。从文章内容来说，也远远没有达到预期目的，还需要更进一步的探索和讨论。

    实际上，从软件工程角度考虑，任何一个软件产品都有一个统领全局的算法机制，如果事先设计好，也会为系统开发和维护带来很大的便利，在设计的时候会有更加清晰的思路和编码方法。但是就本书而言，过多的讨论，反而偏离主线，前后繁复，所以我们暂且把更多的思考放在以后去研究。接下来，让我们把目光投向《侧链》，这也是当前极为火爆的领域。

    参考

    比特币白皮书：一种点对点的电子现金系统

    尼克·萨博《比特金（BitGold）》白皮书

    百度百科关于拜占庭将军问题描述（混淆了两军问题）

    分布式共识难题（英文）)

    拜占庭将军问题深入探讨